CS 110 Lab Project 8

Creating Pictures through Recursion

Due: By 5 p.m. Monday, October 29th

In this lab, we will introduce another library for performing graphics and use it to build some useful functions and to practice with recursion. Why another graphics library you ask? Well, for recursive functions that perform drawing, it is a very helpful thing to have an infrastructure that can perform a set of drawing operations that are relative to the notion of a "current position" on the drawing screen, and to avoid using parameters carrying information about the absolute and global coordinates in which we are drawing. A graphics model known as turtle graphics are perfect for this kind of relative drawing. Also, as it turns out, some of the operations we use in turtle graphics have correspondents in the operations we perform with robots, and we hope to use those later in the semester.

Background: Turtle Graphics and a Template main() function

In turtle graphics, we start with a Screen object, analagous to our GraphWin objects. The coordinate system on a turtle Screen puts the (0,0) point in the center of the screen, like we are used to from a "regular" math coordinate system. Further, y values are positive as we head up (North) on the screen. Coordinates and distances are again measured in screen pixels.

Now imagine a computer/robotic "turtle" starting at (0,0) in the x-y plane. Through Python, we can issue commands (really function invocations) to this turtle, telling it to move forward, turn left or right by a certain number of degrees. As the turtle moves, the movement is animated, and the turtle draws a line showing the path of the given commands, as if the turtle has a pen associated with it. We can also issue other commands like setting the color of the pen, or its line width, and even raising and lowering the pen so that we can move the turtle without the associated drawing taking place.

Just to get a feel for this model, start by bringing up Wing and type the following into the Python shell:

      from turtle import *
      
      world = Screen()
      
      t1 = Turtle()
      t1.forward(100)
      t1.left(120)
      t1.width(2)
      t1.color('red')
      t1.forward(75)
      t1.up()
      t1.forward(25)
      t1.left(60)
      t1.down()
      t1.forward(50)
      
      mainloop()
      

You can find many more functions (methods) for Turtle objects on the Python documentation website, as the turtle library is part of the standard distribution of Python: Turtle Method Documentation

For many of our turtle programs, we structure the top level of our programs in a similar way, so I present a template main() function, within which you can customize for your own needs:

def main():
   winWidth = 250     # Customize for desired width and height
   winHeight = 350    #
   world = Screen()
   world.screensize(winWidth, winHeight)
   
   t1 = Turtle()      # turtle variable can be anything you like.  you could even have multiple turtle objects
   
   # In this section of the main function, you will add invocations to carefully
   # test your function definitions.
   # ...

   mainloop()         # allows the user interface to respond to window resizing, etc.

Problem 1: Practicing with turtles and functions

Write a program in a file named polygon.py. The main() function should use the template from above and then use function invocations to thoroughly demonstrate the functions specified in the list below.

1. Write a fuction called square that takes a parameter named t, which is a turtle. It should use the turtle to draw a square.
2. Add another parameter, named length, to your definition of function square. Modify the body so the length of the sides of the square is length, and then modify the function call to provide a second argument. Run the program again.
3. Next modify the main program to call the input function to get a length from the user, assigning to a variable. Use this length as the argument to the function invocation to square.
4. Make a copy of the square function and change the name to polygon. Add another parameter named n and modify the body so it draws an n-sided regular polygon. Hint: The exterior angles of an n-sided regular polygon are 360.0/n degrees
5. Write a function called circle that takes a turtle, t, and radius, r, as parameters and that draws an approximate circle by invoking polygon with an appropriate length and number of sides. Test your function with a range of values of r.

   Hint: First calculate the circumference given the radius. (Google if you don't remember the calculation for a circle's circumference.) Then compute length by observing that length * n should equal the circumference.

   Another hint: if your turtle (t1) is too slow for you, you can speed him up by changing t1.speed(n), where n is an integer value from 1 to 10, with 1 being slowest and 10 being fastest. Animation can be disabled altogeher with an argument of 0.

6. Make a more general version of circle called arc that takes an additional parameter, called angle, which determines what fraction of a circle to draw. angle is in units of degrees, so when angle=360, arc should draw a complete circle. Note: if this one is giving you trouble, save it for later and move on to the recursive drawing problems described below. ... just don't forget to come back to this one before the due date.
   

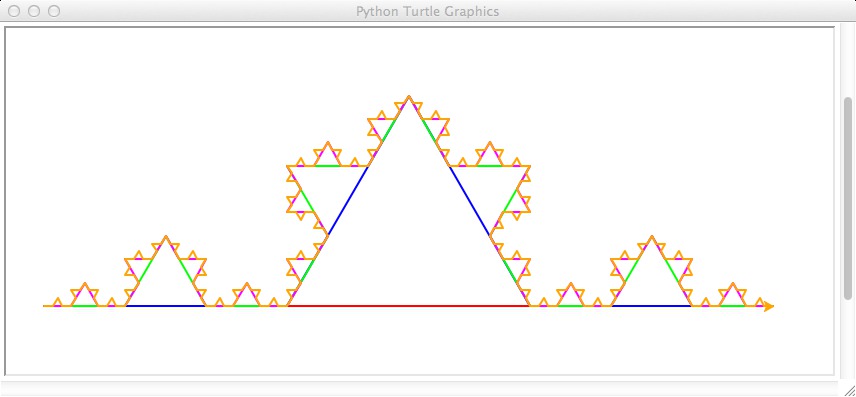
Problem 2: Snowflake

Create a new program called snowflake.py. In the main function, set up for an 800 x 600 turtle screen. Create a Turtle object and set the pen width to 2, and the pen position to (-380, -100) (look for the setpos() function in the documentation).

Create a function called snow() which returns nothing but is given a turtle object and two ints called iteration and length. This function should do one of two things.

• First, if iteration is 0, all you should do is use the forward function on the turtle that was passed in, drawing forward the distance given by length.
• The more complicated case is if iteration is greater than 0. In that case, you will have 7 operations to perform. The first, third, fifth, and seventh operations are all recursive calls to the function snow. Each call will be identical, and will be passed the turtle, iteration-1, and length/3. That is, if we aren’t down to iteration 0 yet, our function will call the snow function four times with a lower iteration value and shorter lengths. This is the part that allows the problem "solved" by our recursive invocations to be smaller instances of the original problem.

  Between each of these recursive calls (i.e., the second, fourth, and sixth operations), we’ll change the direction of our pen. To do this, you’ll use the function left(). The three rotations should be 60, -120 and 60 degrees respectively.

Once you’ve got this, we can test it out. Try calling the function snow in your main function with parameters (t1, 0, 729). (I picked 729 just because it is a power of 3, so when we do integer division by 3 repeatedly, we’ll still have the right integer). You should see a line drawn across most of the image. Try this again, but this time change the iteration to 1. This should add a kink to the middle of the line. Once you have this working, change your main function to make a total of 6 calls to snow, where you start with snow(t1, 0, 729) and go up to snow(t1, 4, 729), incrementing iteration by 1 each time. Between each call, reset the pen position to its starting position, and change the pen color so you can distinguish the lines.

A correct solution should look something like this:

Problem 3: Sierpinski's Carpet

Sierpinski’s carpet is defined as follows. Start with an uncolored square. Split it into 9 equal-sized squares. Color in the middle square. Recursively draw Sierpinski’s carpet in the remaining 8 squares. Here is what you should get:

Create a new program called carpet.py. In the main function, set up for an 729 x 729 turtle screen. Like the snowflake problem above, a recursive function can use a parameter (called iteration above) to control the ultimate depth of the recursion. The base case, where no more recursive calls are made, is when iteration reaches 0. Even in the base case, the drawing of the center square is performed.

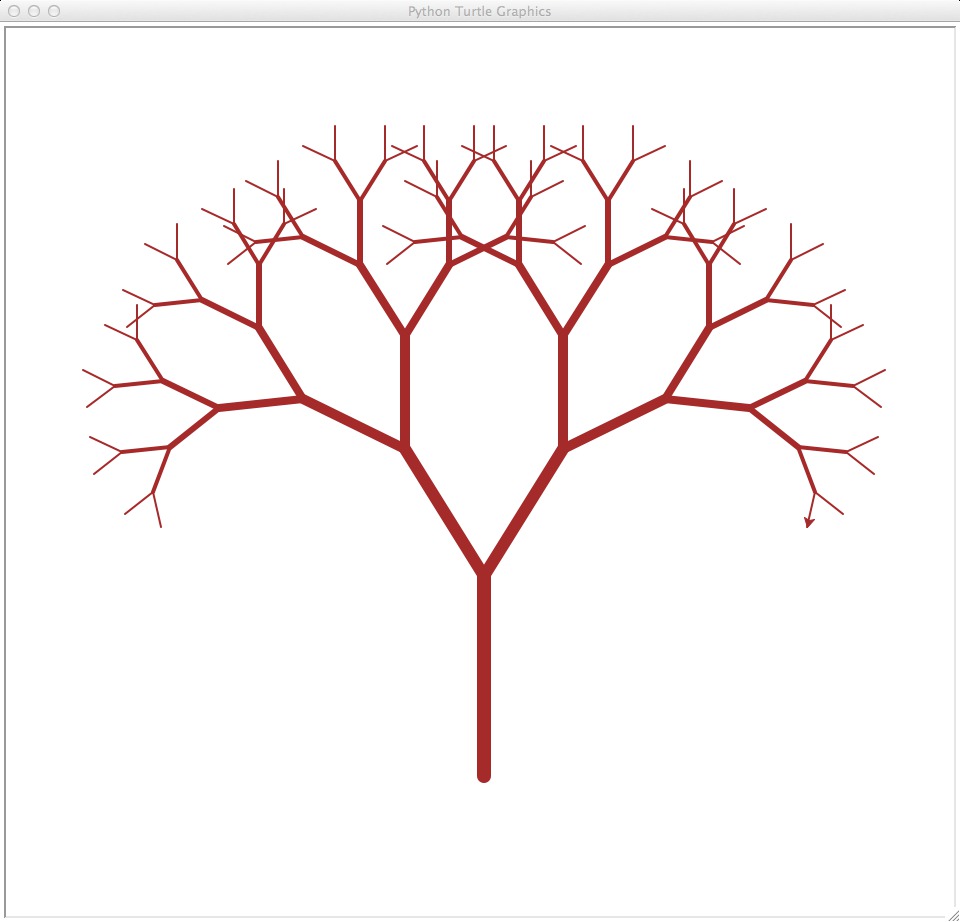
Problem 4: Binary Tree

A Binary Tree is a tree where, at each branching point, we branch into exactly two directions. Binary trees are a great application of recursion, whether we are drawing the tree or have a data structure that utilizes the tree structure. In this case, I give you the picture of the desired result, but I want you to figure out how to use recursion to solve the problem of drawing a binary tree. As in the carpet recursion above, we can use a parameter for governing the depth of the recursion. Part of the problem solving is determining the set of parameters and finding a "consistent" relative position and heading that can be assumed as a precondition to any invocation of the tree() recursive function. Here is what you should get: