Due: Monday, November 9th at class time
In this lab, we'll explore the Game of Life. Invented by mathematician John Conway, the Game of Life is what is called a cellular automaton. It is a set of rules rules which are used to generate patterns that evolve over time. Despite the name, the Game of Life it not a game; it is really a simulation. In some ways, it can be thought of as an extremely simplified biological simulator which produces unexpectedly complex behavior.
The Game of Life is played on an infinite 2D board made up of square cells. It takes way too long to draw an infinite board, so we'll make due with a small finite piece. Each cell can be either live or dead. We'll indicate a live cell as red, and a dead cell as black. The board begins in some initial configuration, which just mean a setting of each cell to be either live or dead (generally we'll start mostly dead cells, and only a few live cells).

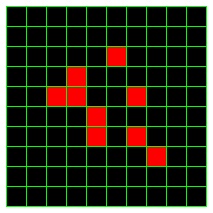
A configuration of a 10-by-10 portion of the board with 9 live cells.
The board is repeatedly updated according to a set of rules, thereby generating a new configuration based on the previous configuration. Some dead cells will become live, some live cells will die, and some cells will be unchanged. This configuration is then updated according to those same rules, producing yet another configuration. This continues in a series of rounds indefinitely (or until you get bored of running your simulation).
The rules are pretty simple: to figure out whether a cell (x,y) will be live or dead in the following round, you just look at the 8 neighbors of that cell (those that share a corner or an edge, so N, S, W, E, NW, NE, SW and SE). What happens to (x,y) next round depends on the number of its neighbors who are live and whether it is currently live or not. In particular:
For example, consider the following 3 initial configurations, and the two configurations that follow.
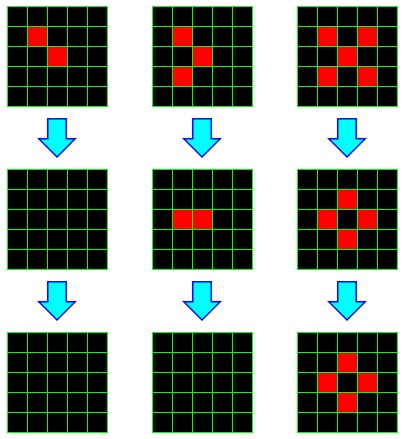
Three initial configurations and two subsequent iterations.
In the first example, both live cells have only one live neighbor, so they both die. Any dead cell has at most two live neighbors, so no new live cells spawn. Thus in one step, there are no live cells. Clearly, at this point, the configuration is stable.
In the second example, two live cells have only one neighbor, so both die. But the third cell lives, and the cell to its immediate left has exactly 3 live neighbors, so it spawns. On the next iteration, we find ourselves in a case similar to the previous example, and all cells die.
In the last example, all currently living cells die; the middle cell has too many neighbors, and the other have too few. However, four dead cells have exactly 3 live neighbors, and so those cells spawn. In the following round, there are neither cells that die nor cells that spawn, so we have a stable configuration. In general, a pattern that doesn't change is called a still-life.
While all of these patterns stabilized quickly, some patterns take a long time to stabilize, and some never do. Of those that never stabilize, some at least have a regularity to them; they eventually eventually repeat states. These are said to be oscillators. Others never repeat the same state again, and produce an infinite number of configurations.
Your first task is to practice (by hand ... with no computer) simulating the Game of Life. Consider the following four intial configurations.
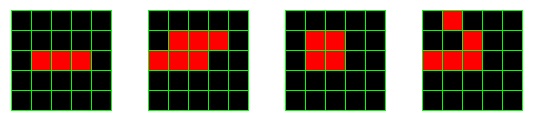
Initial configurations A, B, C and D.
For each of these, you should specify list the intial configuration and the following four generations of each. To record these, use a fixed width font (like courier) and use a period (.) for a dead cell, and an X for a live cell. For example, the initial configurations should look like:
..... ..... ..... .X...List below these the next four generations of each in the same format. Also, indicate how many steps it takes for the configuration to oscillate, if it does repeat itself. Be careful: a pattern that appears again in a different location does not count as an oscillator!
Save your solution as life.rtf.
Write a program called Basics.py that does
all of the following:
- Generates a 20-integer list named A, where each
entry is 0.
- Generates a 50-integer list named B, containing the numbers
from 50 down to 1.
- Generates a 30-integer list named C, containing the
first 30 Fibonacci numbers.
To print the contents of a list A, I would like you to not simply 'print A'; Instead, I would like you to actually loop
through the entries of A and print the elements. Add a few loops to the
above program, after all the lists have been filled, to print the contents of
each list. The contents of each list should be on their own line, and
each entry should be separated by a comma. Make sure you don't have a
comma after the last entry. For example, the first four values for each
list should look like:
List A contains 0, 0, 0, 0, etc.
List B
contains 50, 49, 48, 47, etc.
List C contains 0, 1, 1, 2, etc.
One powerful feature of lists is you can
have multi-dimensional lists. Remember,
A = []
creates an empty list that is referred to by A. The type of the elements of A can be anything, including integers, floats, or strings (which are themselves sequences). So in general, a list named A may have elements that can, themselves be lists.
If we define A to be
A = [ [ 1, 2, 3 ] , [ 4, 5, 6] ]
Then A is a list whose elements are the lists [1, 2, 3] and [4, 5, 6]. We can execute the following in the Python shell once we have the above initialization of A:
>>> print A[0]
[1, 2, 3]
>>> print A[1]
[4, 5, 6]
In Python, we can treat the elements of a list of lists the same way we treat an individual list, so I can do the following:
A[1].append(7)
A[0].append(-2)
print A
and get:
[[1, 2, 3, -1], [4, 5, 6, 7]]
This notion applies to indexing, slicing, and our other operations on lists, so the following is also available to us:
A[0][2] = -5
to assign the value -5 to the index 2 element of the list given by A[0], so when we print A after this, we would get:
[[1, 2, -5, -1], [4, 5, 6, 7]]
When using this notation, we often call the first index (0 in this case) the row index, and call the second index (2 in this example) the column index. If you wrote A as follows:
[1, 2, -5, -1],
[4, 5, 6, 7]]
you can see where this terminology comes from. If I want a list of lists of integers with 7 rows and 5 columns, I can generically create and fill such an array with 0 values as follows:
data = [None] * 7 # creates a list with 8 'None' elements
for row in range(0, 7):
data[row] = [0] * 5 # Each row gets a list of 5 zeros
Write a program called TwoD.py that
creates a 10 row-by-20 column list, and fills cell (row, col) with the value row*col. AFTER
you have filled out the WHOLE list, print this list. You'll probably
need two nested loops to print the list, one to loop over rows and one to loop over columns.
After you've printed the
list, create and initialize a second list, called B, with the same
dimensions. We want to copy the contents of A to B. For reasons we
will see later in class, we don't want to simply say B = A. We also don't
want to simply duplicate the code we had above but replace each A with a
B. Instead, we want to again use loops to copy each entry of A to the
corresponding entry in B. Then use code as you created earlier to print B.
At this point, you should be able to create
and initialize a 2-d list (i.e., a list of lists). You should feel comfortable printing the
contents of the list. And you should understand how to copy the contents
of one list to another. We'll be using all of these pieces to run our
Game of Life simulation.
Let's think about how we might go about setting
up our Life simulator. For starters, we'll want to keep track of our
current board: which cells are alive, and which aren't. We'll encode
these with ints, using 1 to represent live and 0 to represent dead.
Create a new Python program called Life.py. Define two integer
variables height (number of rows) and width (number of columns) to represent the size of our game board. For
now, set the height to 6 and the width to 8. When we refer to the height
or width, we'll use the variable names rather than actual numbers. That
way, if we later decide to change the size of the board, we don't have to search
through our program for all occurences of 6 and 8; we can just change the
initialization of those two variables.
After those variables are
defined, create and initialize a 2-d list of ints called board, with dimensions given by
the corresponding variables. Write a pair of nested loops to print the contents of the
board to the screen. Test this and make sure it works. Encapsulate the printing of an arbitrary 2-d list of ints in a function.
Now we've
got our board set up, we're ready to program the Game of Life. But as
usual, the first step is design. Let's start by thinking about how to
create a single update to the board. At a high level, what we want to do
is simply update every cell in board. But remember, we'll run into
problems if we update one cell and then update the cell next to it, since each
update needs to be done as if none of the others have been done. To solve
this, we'll copy the contents of the board to a second list, and then compute
updates to the original board based on this copy, which won't be changing.
We'll call the second list boardCopy. Now we can view our overall
strategy as follows:
Initialize board and boardCopy.
Assign values
to all cells in board.
Copy contents of board to boardCopy.
Update each
cell in board based on the rules of Life, and referring to boardCopy to count
the number of live neighbors.
Print board.
All these parts should be straightforward at
this point, except the fourth step. To get started here, try to write a
chunk of code that just does the update for a single cell, say
board[4][2]. What is required in a cell update? We first need to
count the number of live neighbors the cell has. And then, use the rules
of the Game of Life to determine what should happen in that cell.
So
first we want to count the number of live neighbors that cell (4,2) has.
We'll be counting by looking at boardCopy, since if we don't, we won't be able
to tell which cells have already changed and which haven't. Remember,
there should be 8 neighbors, including boardCopy[3][1], boardCopy[3][2], etc.,
all the way to boardCopy[5][3]. Notice that since we're representing live
as 1 and dead as 0, all we need to do is compute the sum of these cells to count
the number of neighbors. Nifty, huh? Store the sum in an int
variable called liveCount.
Let's test this out now. Go to the part
of your code where you set all entries in board to 0. Right after that,
manually add a few lines to give values of 1 to some cells in board. In
particular, set (4,2) to 1, and set 3 of its neighbors to 1 as well. Then
go back to your computation of liveCount, and add a line to print liveCount
after it has been computed. Check to make sure that in fact it is
computing the value 3.
Alright, we've counted live neighbors. But
what do we do with this? Well, this number should tell us what to do in
the cell we're focusing on, (4,2). In particular, we'll need to update
that cell in board (or leave it be) depending on what liveCount is, in
accordance with the rules of Life. Use if-statements and the value of
liveCount to set board[4][2] appropriately.
Great. We've just
managed to update one cell in the board. How do we do the whole
thing? Loops you say? Indeed.
We're now going to loop over all (or at least
most) cells in the board and repeat this process. Why only most?
Well, consider cells at the edge of the board, like cell (0,0). Some of
the neighbors of that cell are off the board. If we try to access the
north-west neighbor of this cell, which presumably is (-1,-1), we'll get an
out-of-bounds error. To avoid this issue, we'll only actually update cells
that aren't on the boarder. As such, we'll loop over columns from 1 to
width - 2 (remember width - 1 is the right most column). And similarly,
we'll loop over rows from 1 to height - 2. Replace your update for (4,2)
with code that loops over all these cells (all but the border cells) and do the
update.
Time to test it out. Manually enter a few of the examples
you did on the prelab into board at the beginning of the program. Then run
your program. Does it print the correct next stage? If so, move onto
the next part. Otherwise, you'll need to figure out where things went wrong.
It isn't super easy to see what is happening
with the text view of the game, certainly not compared to pictures like the ones
shown above. Time to fix this.
Let's draw the board on a
graphics object. If we use one pixel per cell, it'll be too hard to see
what is happening. So we'll draw a larger tile for each cell. Define
an int called tileSize, and for now set that to 10. Create a new GraphWin
object, with dimensions (tileSize x width)-by-(tileSize x height). Loop
through all pixels in this image, and set the color of the pixel to red or
black, depending on whether the corresponding cell in board is live or
dead. Hint: To figure out which cell a pixel corresponds to, you should be
able to just use integer division and the tileSize. Alternatively, you can use Rectangle objects and calculate the origin and size of each.
Once that part is
working, try changing the size of the board. Go up to a 20-by-20
board. Check that things still work. Try changing the initial
configuration, and make sure that you see what you expected.
You're now ready to actually run the
simulation in general. We've got all the pieces, we just need to repeat it
over and over again. Define a new integer variable called
iterations. This will tell us how many steps we're going to
simulate. For now, set it to 100.
After the board has been
initialized, create a loop that runs iterations times. Inside the loop,
the following steps should happen:
Copy the board to boardCopy.
Update all cells in board according to boardCopy and the rules of Life.
Update the Picture of the board based on board itself.
Display that
picture.
Run your program. At this point, you should be seeing an
animation of the Game of Life. Play around with the initial
configuration. Try to find some interesting initial configurations.
Make sure you save it with as interesting a starting configuration as possible.
Lab08 should now contain.